先取り学習のメリット

5年生の中学受験を目指す娘。

最近は、オンライン授業から通塾にシフトするなど、頑張っております。

時間の有効活用を求めるなら、オンライン授業は素晴らしいシステムです。

また、塾まで足をつかって通うことにも、オンライン授業では得られない、緊張感やコミュニケーションによる発見があるので、どちらもメリットがたくさんあります。

今後は基本は通塾で、突発的な用事があるときにはオンライン授業に切り替えるなど、臨機応変に対応していこうと思います。

今回は塾で行われた先取り学習の図形について、まとめています。

図形の計算ミスを防ぐこと

塾では、算数の図形を学習しています。

そして、図形の問題を解きやすくするポイントを教えてもらいました。

図形は、中学受験には必須です。

塾の生徒さんで、中学受験を経験した先輩方は、算数は図形が1番難しかったと話していたそうです。

そして、図形は複雑になればなるほど、計算が増えます。

計算が増えれば増えるほど、計算ミスの確率も高くなり、出題形式によっては、1つの計算ミスから、連鎖的にそれ以降の問題についても、間違えた数で計算してしまうなど、大幅に減点されてしまう要因をつくることがあります。

実際に我が家の娘は、毎月おこなわれている学力テストでは、計算ミスから、連鎖的に3問は減点されたことがありました。

1問目の解答から、次の図形問題も計算するなど、初めの答えが分からなければ、次の問題も解けない出題形式のテストでした。

娘に至っては、間違えた数を使い、次の問題もそのまま式をつくり、たて続けに3問のミスをしたことによって、マイナス15点です。

解き方や考え方が正解としても、答えは全て不正解となってしまします。

以上のことから、回答スピードを上げても、計算ミスをしないように、基礎的なトレーニングも大切なことが、分かりました。

そして、過去記事にも書きましたが、できるだけ計算ミスをおこさないようにするためには、分配法則が有効なようです。

塾では、式を簡略化し、計算を少なくできることや、問題を解くスピードや計算の正確性を高めるため、分配法則を使うとされています。

本格的に分配法則を使うのは、中学生になってからですが、塾では小学生から先取り学習をおこなっています。

特に、

図形の面積（円周率も含む）には分配法則が、役立つ

先生は、このようにおっしゃっていました。

図形問題が解きやすくなるポイント

算数の図形を解きやすくするポイントは、

図形をノートに書き写すこと。

こちらは、娘が図形を書き写したノートになります。

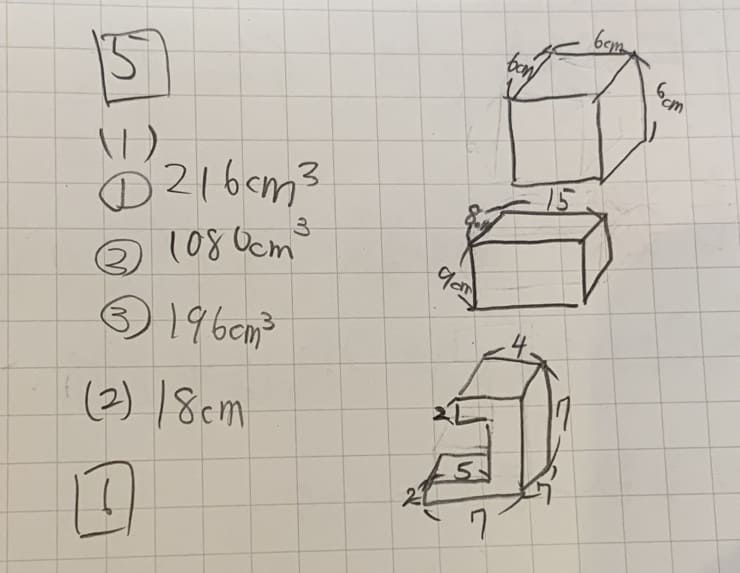
書き写すことによって、答えを導くためのヒントが、見えてくるそうです。

簡単過ぎる多角形の内角の和

そして授業では、多角形の内角の和の求め方を学習しました。

そして、三角形の内角の和は180度と覚えることによって、四角形、五角形、六角形の内角の和も自動的に求められるようになります。

結論から伝えると

（角の数−２）×１８０

※五角形なら「5」とする。

例）五角形

（５ｰ２）×１８０＝５４０度

例）六角形

（６ｰ２）×１８０＝７２０度

上記の式で求められます。

そして、多角形の図形に対角線を引くことによって、計算の仕組みが分かります。

図形に対角線を引くと、

• 四角形は、三角形が２つ
• 五角形は、三角形が３つ
• 六角形は、三角形が４つ
• 七角形は、三角形が５つ
• 八角形は、三角形が６つ

多角の角については、娘のノートにも、五角形と六角形に対角線が引いてあります。

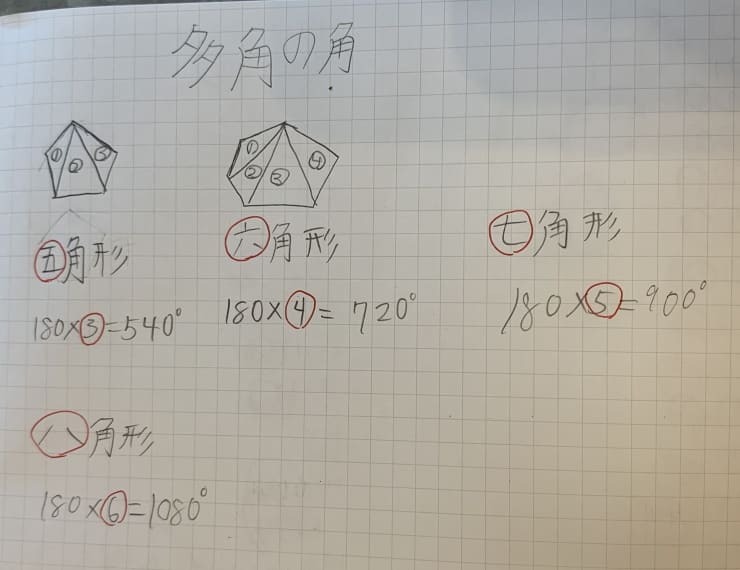
同じように、六角形、七角形も、対角線を引いた三角形の個数×１８０で、内角の和が求められることになります。

この方法で、多角形の内角の和が、驚くほど簡単に求められることが分かりました。

【5年生】角を求める授業

今回の授業の図形は、三角形の外角や、くさび形の角の求め方を習いました。

外角を求める授業

三角形の外角について、娘のノートになります。

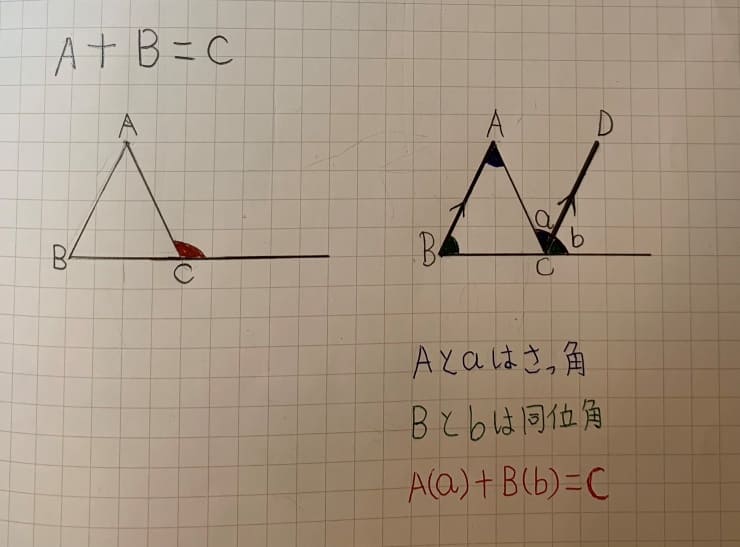
こちらは、∠Ａ、∠Ｂ、を足すと、∠Ｃの外角が求められるという授業です。

そして、同位角と錯覚から求めることができます。

図のように、辺ＡＢに伸ばした直線を引きます。

そして、辺ＡＢと平行な直線を、∠Ｃ、のところから引き、辺ＣＤとする。

上記の平行線を引いたときに、∠Ａと∠ａは錯角で、∠Ｂと∠ｂは同位角となります。

平行線の場合は、同位角と錯角は等しい角度になることから、錯角の∠Ａと∠ａは同じ角度。

同位角の∠Ｂと∠ｂも同じ角度。

よって、∠Ａ、∠Ｂ、を足すと、外角が求められることが分かります。

くさび型の角を求める授業

先生は、板書にはこだわりがあります。

それは板書によって、生徒さんたちの理解が変わるからだそうです。

下画像は、娘のノートの「くさび型」です。

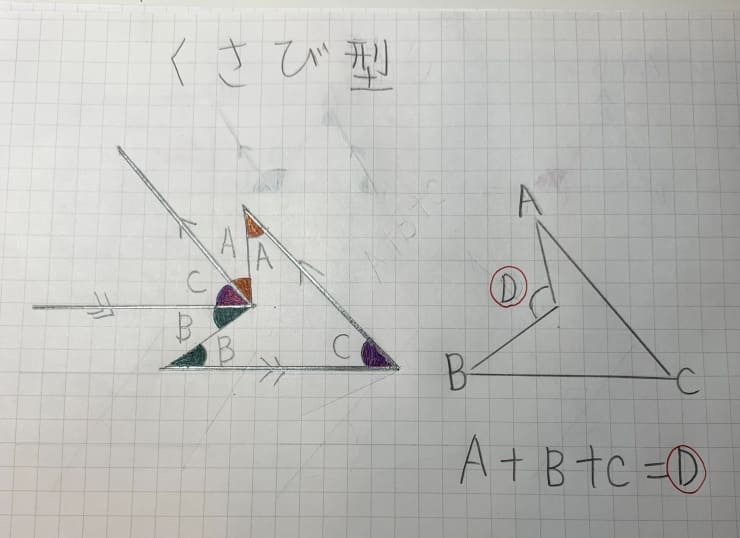
くさび型の角を求めることも習いました。

結論から伝えると、くさび型は、

∠Ａ＋∠B＋∠Ｃ＝∠Ｄ

上記の計算方法で、∠Ｄが、求められます。

前見項目で解説した、三角形の外角の求め方と同じく、錯角と同位角の考え方から、∠Ｄを求めることができます。

理論としては、図のように、辺ＡＣと平行に線を引き、同様に辺ＢＣも平行に線を引くと、同位角が∠Ｃ、錯角が、∠Ａ、∠Ｂとなることが分かります。

同位角と錯覚を足し（∠Ａ＋∠B＋∠Ｃ）、その和が∠Ｄとなります。

夏休みに向けて

5年生ですが算数も、なかなか本格的な授業をおこなうようになってきました。

受験に向けて、知識を日々詰め込んでおります。

こんなに詰め込み過ぎては、頭を振ったら覚えた知識がこぼれ落ちないか心配になりますが。

角の求め方１つをとっても、答えは一つですが、考え方は複数あります。

面積や体積についても同じことがいえるので、やはり図形問題に関しても、思考の柔軟性が問われてくるところです。

まもなく１学期も終わります。

夏休みに入りますが、

「受験は夏休み中が勝負のとき」

先生からは、このように伝えられています。

中だるみしないように生活リズムを整え、この夏を乗り越えていきたいと思います。